Galaxy-brain math: part 1, photos and equivalence classes
I’ve seen it, you’ve seen it, we’ve all seen it. The expanding brain meme.

This meme template is popular and effective because it lets us play with the way we frame things. You start with something very ordinary and keep approaching it from weirder and weirder angles until you end up with something amazing.
I’ve been studying cameras, optics, images, and the mathematics behind it all and recently encountered a new frame for familiar concepts. It actually gave me goosebumps. A truly galaxy-brain interpretation of the geometry behind cameras and perspective.
(Slight digression: it’s moments like these that people think of when they talk about the beauty in mathematics. It was one of those moments that leaves you truly breathless. It’s as though you were hiking uphill all day, sweaty and hunched over under the weight of your backpack until you finally reach the clifftop. You gaze down to the sea below, an endless expanse of azure beneath a silent sky and a dazzling sun. You look to the horizon. The breeze gently traces its fingers through your hair, through the grass at your feet. You may not be religious, but you now understand what it means to see the face of divinity. That’s what it felt like to learn about this sort of geometry for the first time.)

If you’ve ever wondered how vanishing points actually work, you will have a deeper understanding of it by the end of this post.
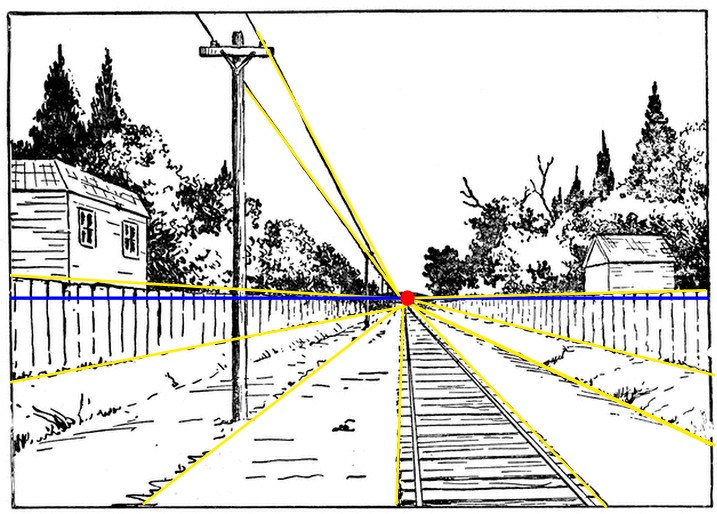
All parallel lines meet at the red dot. That’s the vanishing point. But how can parallel lines meet? You’d think the point of parallel lines was that they don’t.
Mathematical background
In order to fully appreciate what we’re about to see, we will need to begin with some mathematical background. If you know what equivalence classes and cross-products are, you know enough to skip this section.
Geometry: points, lines, rays, planes, spaces
We'll be using the basic language of geometry to describe how images appear on flat surfaces. The internet is filled with introduction to geometry tutorials if you want to brush up. Don't worry too much about fancy theorems, just understand what points, lines, rays, planes and spaces are.
Set theory: from elements to equivalence classes
Sets are collections of objects. We refer to these objects as "elements" or "members" of the set. We can speak of the set containing all dogs in the world, or maybe the set containing the letters in the English alphabet, or the set that contains no elements at all. The set of all numbers greater than 3.5, the set of all odd numbers, the set of all triangles, the empty set (which contains no elements at all). The set containing only the numbers 2 and 4 would be written as {2, 4}.
Ordered pairs: If we start with a set A = {1, 4} and a set B = {2, 3} then we can make ordered pairs of elements, one element from A and one element from B. For instance, we could have the ordered pair (1, 2). The element order matters here! (1, 2) is different from (2, 1).
Binary relation: If we have a bunch of ordered pairs made of an element from set A and an element from set B, we can start thinking about a set of such ordered pairs. For instance, the set R = {(1, 2), (4, 3), (4, 2)} is a set containing only those types of ordered pairs. We call any set like R (which only contain these types of ordered pairs) a binary relation over A and B. Binary relations are a useful way to think about many things in math. If we call the set of all integers Z, as mathematicians do, then we can have a binary relation E over Z and Z containing only these ordered pairs: (0, 0), (1, 1), (-1, -1), (2, 2), (-2, -2), (3, 3), (-3, -3), ... etc. This binary relation E is more commonly known as equality, because for every single ordered pair we can write a (rather obvious) equation: 0 = 0, 1 = 1, -1 = -1, etc.
Equivalence relation: Equivalence relation are special binary relations. Because of their special properties, they're interesting to consider. Specifically, they're reflexive, symmetric, and transitive (the internet is filled with good explanations of what those words mean).
Equivalence relations divide their set into subsets that share no members in common-- the subsets do not intersect with each other. These subsets are called equivalence classes. In math, equivalence classes are cool. If you notice equivalence classes when you weren't looking for them, you jump in the air and pump your fist and celebrate. They are Inherently Cool. If you're taking care of a mathematician with the flu, you should whisper the words "equivalence class" into their ear after you've fed them soup and tucked them into bed.
A good way to think about equivalence classes is that each equivalence class has some underlying theme or idea. An equivalence relation that partitions the integers into odd numbers and even numbers makes for two equivalence classes: the odds and the evens. Each subset has a neat, underlying idea running through them; every number in the set of odd integers is not divisible by 2, and every number in the set of even integers is. The value in thinking equivalence classes is that they give us a hint towards interesting underlying ideas in the sets that we study. That's why equivalence classes are important.
Rays of light
When we take a 3-D object and represent it on a 2-D surface, it’s called a projection. It’s what cameras do. They take the world and project it onto a photograph. For our purposes, the surface we’re projecting things onto is a plane. It’s perfectly flat like a piece of paper or a photograph. We’ll call it the projective plane (or image plane).
If we think in terms of rays of light, you’ll notice that the rays of light go from a point on the object to the camera. The line also goes through the corresponding point in the projective plane. In fact, almost every point in space has a ray of light that goes from it through the projective plane to the point where the camera is.
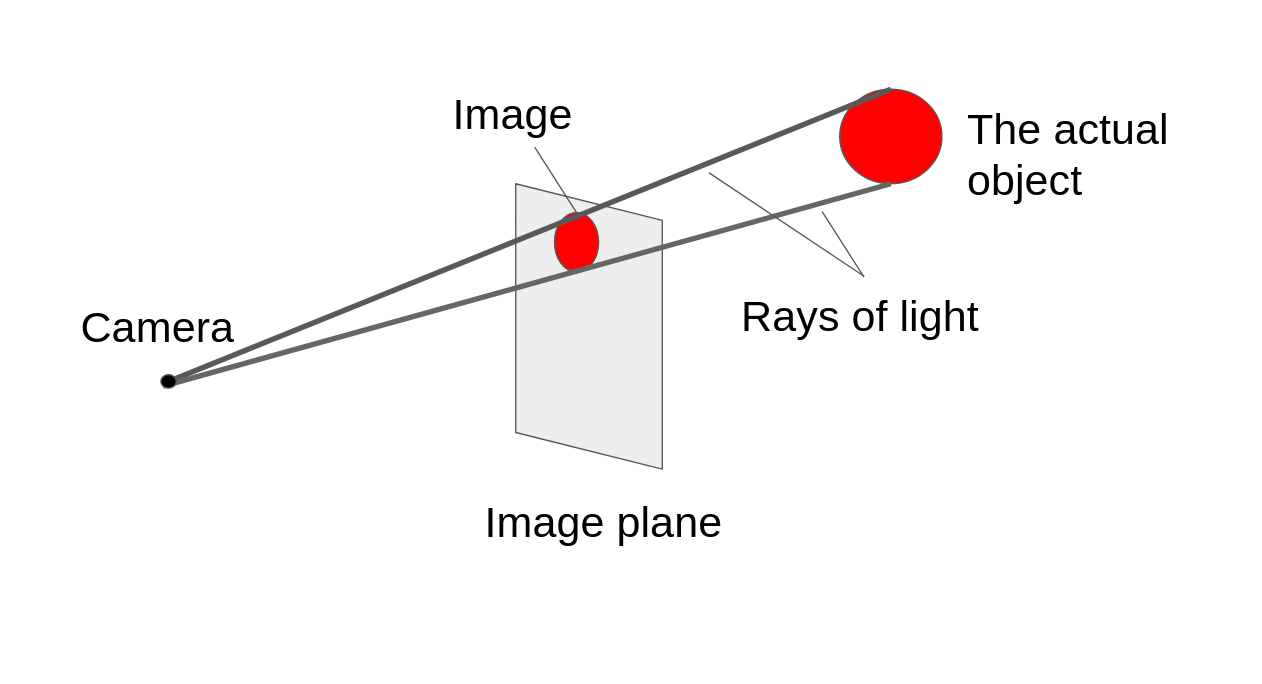
“Wait, but what about points behind the camera? That straight line doesn’t go through the projective plane!”
As it turns out, these points also have a ray of light associated with them. You just have to extend the ray-of-light idea a little bit:
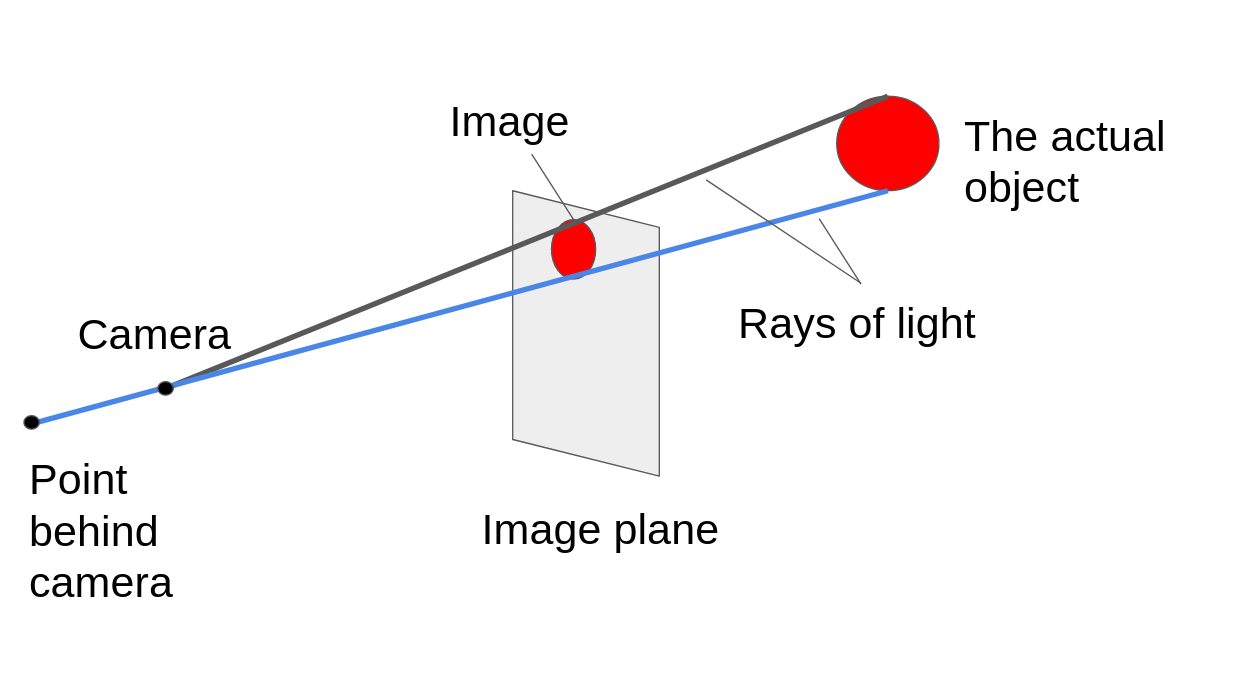
“Hold on– but you said almost every point. Which point doesn’t have a line to the camera going through the projective plane then?”
And the answer to that is the point where the camera is. There is no ray of light going from the camera to the camera, because they’re the same point! But for every other location in space, we have a ray of light going from that location straight to the camera, and that ray of light goes through the projective plane.
Each ray of light goes through the projective plane in exactly one spot. I’ve labeled the intersection for one such ray in green.
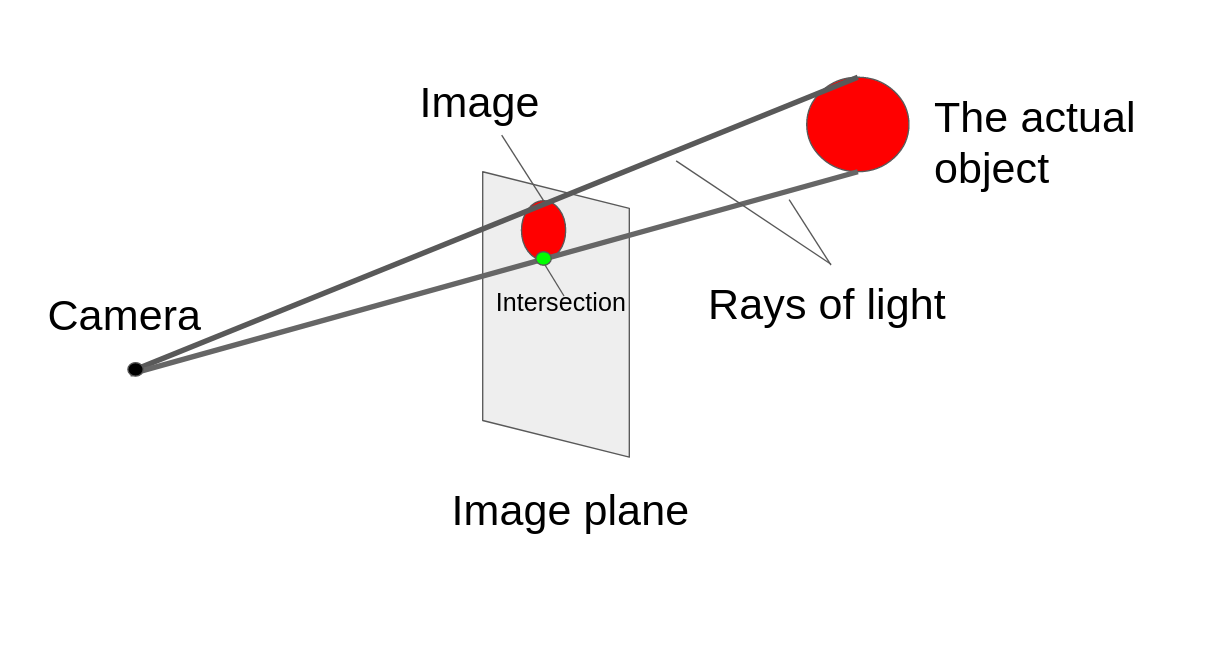
To recap: we’ve figured out a deep relationship between these rays in 3-D space and points on the projective plane. Each ray has one, and exactly one, corresponding point on the projective plane.
Next, we’ll turn our attention to points on the same ray of light. Remember how equivalence classes often have some sort of interesting underlying trait? Here, we can think of a ray of light as an equivalence class. The equivalence class contains all the points on that ray (minus the camera’s location). All the points in the same equivalence class are related to each other because they’re somewhere on the same beam of light!
What does this mean? Well, we know that every point on the projective plane corresponds to exactly one ray. We also know that every ray is an equivalence class containing all the points on it (except, of course, the camera’s location).
Therefore:
Every point on the projective plane corresponds to an equivalence class made from its ray of light. The projective plane as a whole is the set of all such equivalence classes because every ray of light goes through the projective plane in exactly one point.
What does this tell us?
Well, it explains why we can’t see behind objects, because two objects that are on the same ray of light would show up at the same point on the projective plane. If you stand behind a brick wall and someone takes a picture, all the photograph will show is the brick wall.
That might be a rather obvious observation to anyone who’s actually taken a photo of anything (or used their eyes), but it’s fine to start from what seems obvious because we’re starting to see how math can explain familiar ideas from a completely new perspective.
In Part 2, we’ll reframe some very basic ideas from geometry. Stay tuned!